Recurrent Neural Networks(RNNs)

Sequential Data:

Sequential Data are such data where the order of elements is matter
Elements are dependent on the previous ones
Example:

- Time Series Data: Data points collected or recorded at specific time intervals, such as stock prices, temperature readings, or heart rate monitoring.
- Text Data: Sequences of words or characters, where the meaning of a word can depend on the words that come before it.
- Speech Data: Audio signals that vary over time, where the sequence of sounds forms words and sentences.
- Video Data: A sequence of frames (images) that, when played in order, create a moving picture.
- DNA Sequences: Biological sequences where the order of nucleotides is crucial for the genetic information they carry.

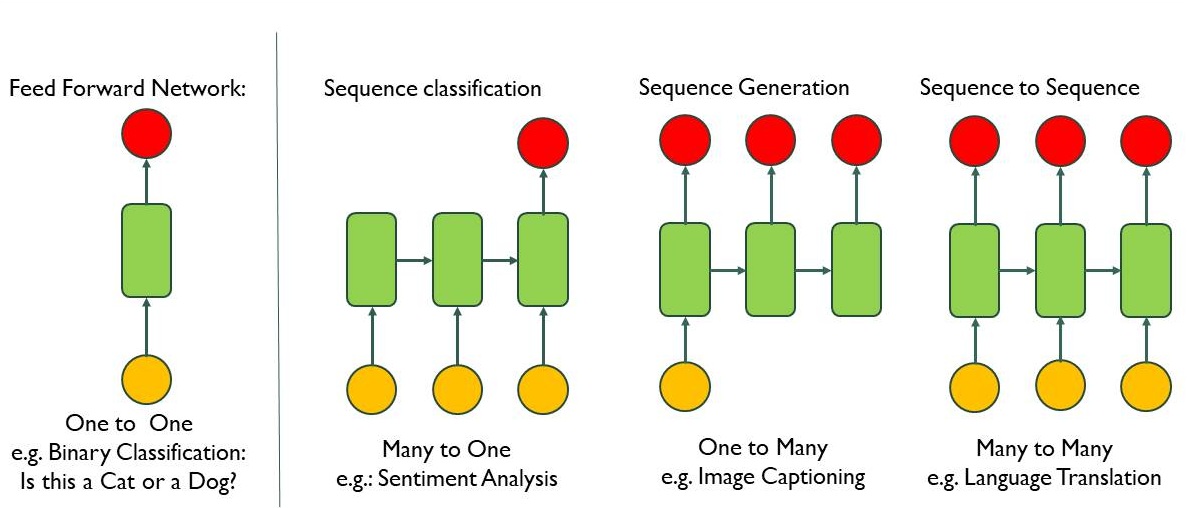
Applications of Sequence Modelling:

While basic neural network (Vanilla Neural Network) gives single output from single input as in image below from left first one which is simple neural network, Sequence model can do below 3 operations :

Many input to one output : Process the many words in the individual sentences & produce a output. For example, sentiment analysis where sentences could have positive or negative reviews.
One input to many output : Taking one image & produce caption of the image which is sentence of many words. For example, image captioning.
Many input to many output : Taking a sentence with many words & produce another sentence with many words. For example, Translation from one language to another language.

The term “Vanilla Neural Network” means the most basic neural network – also known as a Feedforward Neural Network (FNN) or Multilayer Perceptron (MLP).

Neurons with Recurrence:

We will now see the transition from a simple, memoryless model (vanilla NN) to a dynamic model (RNN) that captures time dependencies by recycling hidden states across time.

Start with a Vanilla Neural Network
- Imagine a basic feedforward neural network (vanilla NN) where input flows from left to right (or bottom to top if rotated).
Apply it to Sequential Data
- Sequential data has multiple time steps (e.g., t0, t1, t2, etc.).
- Initially, we might think of running the same neural network on each time step independently (treating each as an isolated input-output pair).
Identify the Problem
- When we process each time step independently, the model ignores the relationship between time steps.
- In sequential data (like text, stock prices, speech), the current prediction depends on previous data. Ignoring past time steps leads to poor modeling of the sequence.
Introduce the Concept of Memory
- To address this, you need a way to “remember” past information.
- The solution is to pass information forward in time within the network using an internal state.
Define an Internal State (hₜ)
- Introduce a hidden/internal state variable h(t).
- h(t) acts like a memory cell that holds information about past computations (e.g., what happened at t0 and t1 when computing output at t2).
New Output Dependency
- Now the output ŷ(t) at time step t depends on:
  - The current input x(t)
  - The internal state h(t-1) passed from the previous time step.
Formula: Yt = f ( Xt , ht-1 )
Recurrence Relation
- This recursive dependency (passing h(t) forward in time) creates a recurrence relation, meaning the computation at time t is influenced by past computations.
Visualization
- Unrolled View: Time steps are laid out as a sequence, and h(t) connects each time step like a chain.(reader right of end of the video)
- Loop View: Represented as a looped diagram showing the hidden state feeding back into itself across time steps.(reader left of end of video)
Recurrent Neural Networks
- This architecture forms the foundation of Recurrent Neural Networks (RNNs).
- Unlike a vanilla NN, an RNN maintains internal memory and is capable of capturing temporal dependencies within sequential data.

Please click on video to see visualization of above explanation

Definition of RNNs:

An RNN (Recurrent Neural Network) is a type of neural network that is specifically designed to handle sequential data.
Unlike traditional feedforward neural networks, which process inputs independently, an RNN introduces loops within the network.
These loops enable information to persist, meaning the output of a neuron at a one-time step is fed back into the network as input at the next time step.

This feedback mechanism creates a form of short-term memory—allowing the network to retain contextual information from previous inputs, which is critical when dealing with time-dependent data, text data, etc.

RNN Architecture Overview:

At its core, an RNN processes input sequences step-by-step, maintaining a hidden state vector that captures information about previous elements in the sequence.

Each time step has:

Input (xₜ): The data at time step t.
Hidden State (hₜ): The “memory” carried from one-time step to the next.
Output (yₜ): The prediction or processed value at time t.

The hidden state is updated using the formula:

h_ₜ = f_w(x_ₜ , h_ₜ₋₁)

Here,

h_{ₜ =}New state

x_{ₜ =}Input vector

h_{ₜ₋₁ =}Old State

f_{w =}Activation Function

Also we can write as, hₜ = f(Wₓ * xₜ + Wₕ * hₜ₋₁)
Where Wₓ and Wₕ are learned weight matrices, and f is an activation function like tanh or ReLU.

For a simple RNN we can write as below:

Unfolding RNNS :

Let’s unfold RNN network to understand better

W_xh is weight matrics that transformed input to the computational hidden state
W_hh is weight matrics that update hidden state
W_hy is weight matrics that transformed the hidden state to the output
Importantly these are same weight matrices at every time step & they reuse at every time step in the sequence
We want to adjust the RNN’s weights so that its predictions are as close as possible to the actual targets .
To do this, we need a loss function.
Just like any neural network, we need a way to measure how wrong the RNN’s predictions are.
This is done by calculating a loss at each time step.
RNN makes a prediction at every time step (ŷₜ).
We compare it to the correct answer (yₜ) at that time step.
We do this for all time steps in the sequence & calculate total loss
This total loss is what we minimize when training the RNN.
Making predictions step-by-step through time (T₀ > T₁ >T₂ … > Tₜ).
This is called the forward pass.

Please click on video to see visualization of above explanation

Sequence Modeling: Design Criteria

Sequence models need to do-

Variable-length handling:
- Sequences can be short or long (e.g., one sentence vs. a full paragraph).
Track long-term dependencies:
- Understand relationships far apart in the sequence (e.g., the subject at the start of a sentence and its verb much later).
Maintain order:
- Sequences are ordered. “The cat sat” ≠ “Sat the cat”.
Share parameters:
- The model uses the same weights at every time step, making it efficient and generalizable.

Why RNNs fit the above design criteria:

RNNs loop back on themselves to process each input step-by-step, maintaining memory (hidden state).
This looping structure allows them to:
- Handle any length.
- Remember past steps (though not always perfectly).
- Keep track of sequence order.

Sequence Modelling Problem: Predict the Next Word

Let’s Demonstrate a sequence modeling problem step-by-step where the goal is to predict the next word in a sentence.

Given the sentence “The cat is sitting on the” and our goal is to predict the next word.

Task:
- Input: A sequence of words (e.g., “The cat is sitting on the”).
- Output: The most likely next word (e.g., “mat”, “floor”, “sofa”, etc.).
- Type of Model: Sequence-to-One (sequence in → single prediction out).
Encoding language for a Neural Network:
- Vocabulary: Corpus of words with all possible words we could encounter
- Word Indexing: taking individual words from vocabulary & map them into index number
  - - - the → 1
        cat → 2
        … → …
        mat → N
- Embedding: Transform indexes into a vector of fixed size by One Hot Encoding

Please click on video to see visualization of above explanation:

What is a Semantic Space?

A semantic space is a vector space which encodes ‘meanings’ of words
Words embedded in vectors that are similar in meaning or used in similar contexts are placed closer together in this space.
Think of it like a map where:

- Paris and London are near each other.
- Paris and Banana are very far apart.

RNNs from Scratch in Tensorflow:

# Import necessary libraries
import tensorflow as tf
from tensorflow.keras.layers import Layer

# Define custom RNN Cell
class MyRNNCell(tf.keras.layers.Layer):
    def __init__(self, rnn_units, input_dim, output_dim):
        super(MyRNNCell, self).__init__()

        # Save dimensions for later use 
        self.rnn_units = rnn_units
        self.input_dim = input_dim
        self.output_dim = output_dim

        ## Initialize weight matrices 

        # W_xh: maps input to hidden state
        self.W_xh = self.add_weight(shape=(rnn_units, input_dim), initializer='random_normal')
        
        # W_hh: maps previous hidden state to next hidden state (recurrent connection)
        self.W_hh = self.add_weight(shape=(rnn_units, rnn_units), initializer='random_normal')
        
        # W_hy: maps hidden state to output
        self.W_hy = self.add_weight(shape=(output_dim, rnn_units), initializer='random_normal')

        # Initialize Hidden state to zeros
        self.h = tf.zeros([rnn_units, 1])

    # Define forward pass (call is like "run" for the layer)

    def call(self, x):

         # update hidden state, h_t = tanh(W_hh * h_{t-1} + W_xh * x_t)
        self.h = tf.math.tanh(tf.matmul(self.W_hh, self.h) + tf.matmul(self.W_xh, x))

        # Compute the output, Output = W_hy * h_t
        output = tf.matmul(self.W_hy, self.h)

         # Return the current output & hidden state
        return output, self.h

Python Implementation for RNN

# Import Necessary libraries
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import SimpleRNN, Dense

# ====== STEP 1: Generate Sample Retail/Fashion Data ======
# Let's simulate daily sales data for a fashion item (e.g., T-shirt sales)
# We'll create a simple synthetic dataset: 500 days of sales

np.random.seed(42)

total_days = 500
sales_data = np.random.randint(20, 100, size=(total_days,))  # sales between 20 and 100 units/day

# ====== STEP 2: Preprocess Data into Sequences ======
# We will use the past 7 days (window) to predict the next day

window_size = 7

X_train = []
y_train = []

for i in range(len(sales_data) - window_size):
    X_train.append(sales_data[i:i + window_size])
    y_train.append(sales_data[i + window_size])

X_train = np.array(X_train)
y_train = np.array(y_train)

# Normalize sales data
X_train = X_train / 100.0
y_train = y_train / 100.0

# Reshape for RNN input: (samples, timesteps, features)
X_train = X_train.reshape((X_train.shape[0], X_train.shape[1], 1))

# ====== STEP 3: Build RNN Model using TensorFlow/Keras ======

model = Sequential([
    SimpleRNN(32, activation='tanh', input_shape=(window_size, 1)),  # 32 hidden units
    Dense(1)  # Output Layer)
])
# ====== STEP 4: Compile the model ======
model.compile(optimizer='adam', loss='mse')

# ====== STEP 5: Train the Model ======
model.fit(X_train, y_train, epochs=20, batch_size=16,verbose=0)

# ====== STEP 6: Evaluate the model ======
loss = model.evaluate(X_train, y_train)
print(f'----------Loss----------\n {loss}')

# ====== STEP 7: Make Predictions ======
# Let's predict the sales for the next day given the last 7 days

latest_window = sales_data[-7:] / 100.0  # normalize latest 7 days
latest_window = latest_window.reshape((1, window_size, 1))  # reshape to match model input

predicted_sales = model.predict(latest_window)
predicted_sales = predicted_sales[0][0] * 100.0  # rescale back to original sales range

print("\nPredicted sales for next day:", round(predicted_sales, 2), "units")

# ====== STEP 8: Predict on Training Data for Visualization ======

predictions = model.predict(X_train).flatten() * 100.0  # rescale predictions back
true_sales = y_train * 100.0  # rescale true values back

# ====== STEP 9: Plot true sales vs model predictions ======

plt.figure(figsize=(7, 5))
plt.plot(range(len(true_sales)), true_sales, label='True Sales (Next Day)')
plt.plot(range(len(predictions)), predictions, label='Predicted Sales (Next Day)')
plt.title('Retail Sales and SimpleRNN Predictions')
plt.xlabel('Time Step (Days)')
plt.ylabel('Sales Units')
plt.xlim(450, 457)
plt.legend()
plt.grid(True)
plt.show()

Output:
16/16 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.0529  
----------Loss----------
 0.05076256021857262
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 220ms/step

Predicted sales for next day: 61.05 units
16/16 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step